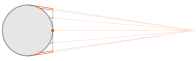| Name | Author, Date | Example, with relevant parameters | Also known as /
[Equivalent to] | Properties | Equal-Area? | Used by /
[Applications] |
| Equidistant Cylindrical | attributed to Marinus of Tyre, c.100 CE | 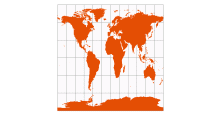
standard parallels: 60° N/S, 30° N/S, 0° | Equirectangular
[Equidistant Conic with standard parallels equidistant from the equator] | All merdians are standard, with same scale as the standard parallels
No distortion along standard parallels | | Mapquest (standard parallels 37.5° N/S)
Yahoo Maps (standard parallels 51° N/S) |
| Plate Carrée (literally, “plane square”) | known since antiquity
renamed “carte plate carrée” by M. Armard P. d'Avezac-Macaya, 1863 | 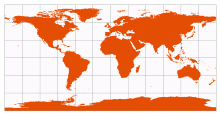 | Plane Chart
[Equidistant Cylindrical with standard parallel at 0°] | All merdians are standard, with same scale as the equator
No distortion along equator
Lat/Lon lines make squares
Boundary is a 2:1 rectangle | | National Geographic’s online MapMachine |
Werner
(in ArcMap, use Bonne) | based on Ptolemy’s 2nd Projection, c.100 CE
final form by Johannes Stabius (c.1500), promoted by Johannes Werner (1514) | 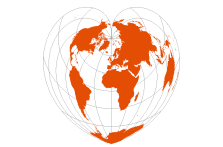 | Cordiform (“heart-shaped”)
[Bonne with reference parallel at 90°N] | All parallels are standard, with the same scale as the central meridian
Parallels are concentric circles about the North Pole
No distortion along the central meridian | Equal-Area | ♥ |
| Bonne | based on Ptolemy’s 2nd Projection, c.100 CE
final form by Rigobert Bonne, c.1752 | 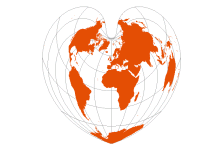
reference parallel: 60°N, 90°N, 30°N, 0° | Cordiform (“heart-shaped”) | All parallels are standard, with the same scale as the central meridian; parallels are concentric circles
No distortion along the reference parallel or the central meridian
Special Cases: Werner results when the reference parallel is at a pole. Sinusoidal results when the reference parallel is at the equator. | Equal-Area | ♥ |
| Sinusoidal | used in various atlases, c.1600
renamed “sinusoidal” by M. Armard P. d'Avezac-Macaya, 1863 | 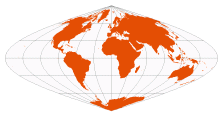 | Sanson-Flamsteed
Mercator Equal-Area
[Bonne with reference parallel at 0°] | All parallels are standard, with the same scale as the central meridian
No distortion along the equator or the central meridian — this is the only equal-area projection with equally spaced horizontal parallels
Meridians are half-period sinusoids | Equal-Area | |
| Mercator | Gerardus Mercator, 1569 | 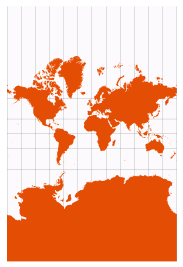 | Cylindrical Conformal
[Lambert Conformal Conic with standard parallels at or equidistant from the equator] | Conformal: local angles are preserved, and local circles are not deformed — at every point east/west scale is the same as north/south scale
Distortion is constant along any parallel, and any parallel can be defined as standard
Constant bearings (rhumb lines / loxodromes) are straight lines
Map extends infinitely North and South | | Google Maps (note the dynamic scale bar)
[navigating a constant bearing] |
| Miller Cylindrical | Osborn Miller, 1942 | 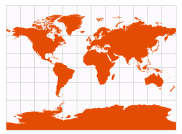 | [modified Mercator] | Pleasant balance of shape and scale distortion
No distortion along the standard parallel at the equator
Unlike Mercator, this map is finite (but not conformal) | | Various American atlases |
| Gall Stereographic | James Gall, 1885 | 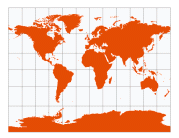 | | 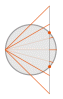
No distortion along the standard parallels at 45° N/S | | National Atlas of the USSR (1937)
Rand McNally
Various British atlases |
| Times | John Moir, 1965 | 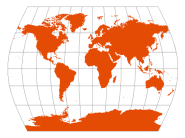 | [parallels from Gall Stereographic, meridians curved to reduce distortion] | Pleasant balance of shape and scale distortion
Standard parallels at 45° N/S; distortion-free only where the standard parallels intersect the central meridian | | Bartholomew Ltd., The Times Atlas |
| Mollweide | Karl Mollweide, 1805
popularized by
Jacques Babinet, 1857 | 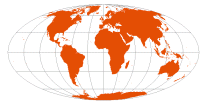 | homolographic
elliptical
Babinet | Standard parallels at 40º 44' N/S; parallels are unequal in spacing and scale; distortion-free only where the standard parallels intersect the central meridian
Meridians are half-ellispses; boundary is a 2:1 ellipse | Equal-Area | |
| Aitoff | David Aitoff, 1889 | 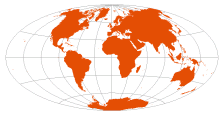 | [expanded Azimuthal Equidistant with central point at 0°/0°] | Pleasant balance of shape and scale distortion
Boundary is a 2:1 ellipse
No standard lines; distortion-free only at central point | | superceded by Hammer-Aitoff |
| Hammer-Aitoff | Ernst Hammer, 1892 | 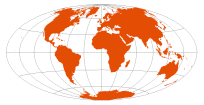 | Hammer
[expanded Lambert Azimuthal Equal-Area with central point at 0°/0°] | Pleasant balance of shape and scale distortion
Boundary is a 2:1 ellipse
No standard lines; distortion-free only at central point | Equal-Area | |
| Goode Homolosine | J. Paul Goode, 1923 | 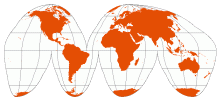
interrupted to show: land, ocean | [Sinusoidal between 40° 44' 11.8" N/S, Mollweide at higher latitudes] | Developed as a teaching replacement for the “evil Mercator” projection.
No distortion along the equator or the vertical meridians in the middle latitudes | Equal-Area | USGS
Many school atlases |
| Craster Parabolic | John Craster, 1929 | 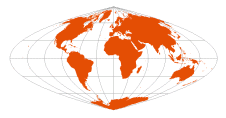 | Reinhold Putniņš P4 (1934) | Standard parallels at 36º 46' N/S; parallels are unequal in spacing and scale; distortion-free only where the standard parallels intersect the central meridian
Central meridian is half the length of the equator
Meridians are parabolas | Equal-Area | |
| Quartic Authalic | Karl Siemon, 1937
Oscar Adams, 1944 | 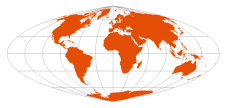 | | Standard parallel at 0°; parallels are unequal in spacing and scale; no distortion along the equator
Following the equatorial Lambert Azimuthal Equal-Area, equator is π/sqrt(2) times the length of the central meridian
Meridians are fourth-order curves | Equal-Area | |
| Cylindrical Equal-Area | Johann H. Lambert, 1772 | 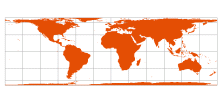
standard parallels: 0°, 30° N/S, 45° N/S | Lambert Cylindrical Equal-Area
[Albers Equal-Area Conic with standard parallels equidistant from the equator] | 
Parallels are exactly π times the length of meridians
No distortion along the standard parallels
Behrmann, Gall-Peters, and Hobo-Dyer are derivatives of this projection
These are the only rectangular equal-area projections | Equal-Area | |
| Behrmann | Walter Behrmann, 1910 | 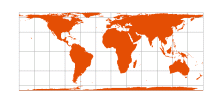 | [Cylindrical Equal Area with standard parallels at 30° N/S] | 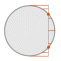
note | Equal-Area | |
Hobo-Dyer
(in ArcMap, use Cylindrical Equal-Area) | Mark Dyer, 2002 | 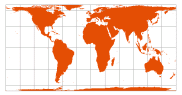 | [Cylindrical Equal Area with standard parallels at 37.5° N/S] | 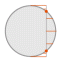
note
often plotted with South up
“Hobo” comes from the first names of Howard Bronstein and Bob Abramms, founders of ODT, Inc. (Amherst, MA mapsellers). | Equal-Area | ODT, Inc.
Carter Foundation |
Gall-Peters
(in ArcMap, use Cylindrical Equal-Area) | James Gall, 1855
Arno Peters, 1967 (presented 1973) | 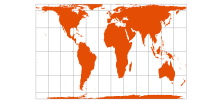 | Gall Orthographic
Peters
[Cylindrical Equal Area with standard parallels at 45° N/S] | 
note | Equal-Area | UNESCO
NATO
Vatican
World Council of Churches |
| Van der Grinten I | Alphons J. van der Grinten, 1898
(published 1904) | 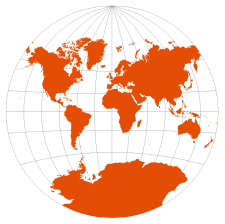 | | Pleasant balance of shape and scale distortion
Boundary is a circle; all parallels and meridians are circular arcs (spacing of parallels is arbitrary)
No distortion along the standard parallel at the equator
Usually clipped near 80° N/S | | National Geographic (1922-1988)
US Dept of Agriculture (from 1949) |
| Eckert I | Max Eckert, 1906 | 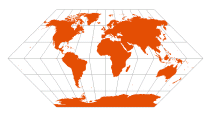 | | Standard parallel at 0º; parallels are equally spaced; distortion-free only at central point
Pole-lines and central meridian are half the length of the equator | | |
| Eckert II | Max Eckert, 1906 | 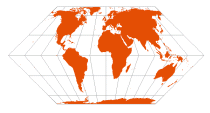 | | Standard parallels at 55º 10' N/S; parallels are unequal in spacing and scale; distortion-free only where the standard parallels intersect the central meridian
Pole-lines and central meridian are half the length of the equator | Equal-Area | |
| Eckert III | Max Eckert, 1906 | 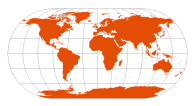 | [Winkel II with standard parallel at 0° — mathematical average of Plate Carrée and Mollweide] | Standard parallel at 0º; parallels are equally spaced; distortion-free only at central point
Outer meridians are semicircles; other meridians are semiellipses
Pole-lines and central meridian are half the length of the equator | | |
| Eckert IV | Max Eckert, 1906 | 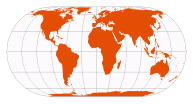 | | Standard parallels at 40º 30' N/S; parallels are unequal in spacing and scale; distortion-free only where the standard parallels intersect the central meridian
Outer meridians are semicircles; other meridians are semiellipses
Pole-lines and central meridian are half the length of the equator | Equal-Area | National Atlases of the USSR (1937) and Japan (1977)
National Geographic |
| Eckert V | Max Eckert, 1906 | 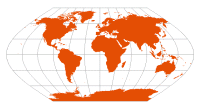 | [Winkel I with standard parallel at 0° — mathematical average of Plate Carrée and Sinusoidal] | Standard parallel at 0º; parallels are equally spaced; distortion-free only at central point
Meridians are half-period sinusoids
Pole-lines and central meridian are half the length of the equator | | |
| Eckert VI | Max Eckert, 1906 | 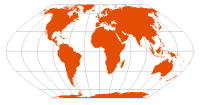 | | Standard parallels at 49º 16' N/S; parallels are unequal in spacing and scale; distortion-free only where the standard parallels intersect the central meridian
Meridians are half-period sinusoids
Pole-lines and central meridian are half the length of the equator | Equal-Area | |
| Winkel I | Oswald Winkel, 1914 | 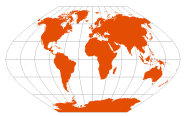
standard parallels at ~50° 27' 35" N/S | [mathematical average of Equirectangular and Sinusoidal — the generalization of Eckert V] | Pleasant balance of shape and scale distortion
Distortion-free only where the standard parallels intersect the central meridian
with Winkel’s preferred standard parallels ±arccos(2/π), total map area is appropriately π × the length of the equator | | |
| Winkel II | Oswald Winkel, 1918 | 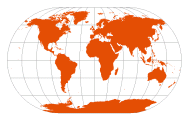
standard parallels at ~50° 27' 35" N/S | [mathematical average of Equirectangular and Mollweide — the generalization of Eckert III] | Pleasant balance of shape and scale distortion
Distortion-free only where the standard parallels intersect the central meridian | | |
| Winkel Tripel | Oswald Winkel, 1921 | 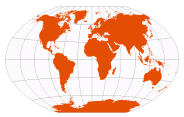
standard parallels of component Equirectangular at ~50° 27' 35" N/S | [mathematical average of Equirectangular and Aitoff] | Pleasant balance of shape and scale distortion
Unlike other Winkel projections, there are no standard parallels on the final map
No point is distortion-free | | The Times Atlas
National Geographic (since 1998) |
| Flat Polar Quartic | Felix W. McBryde and Paul Thomas, 1949 | 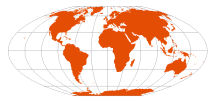 | McBryde-Thomas #4 | Standard parallels at 33º 45' N/S; parallels are unequal in spacing and scale; distortion-free only where the standard parallels intersect the central meridian
Pole-lines are one-third the length of the equator, equator is π/sqrt(2) times the length of the central meridian
Meridians are fourth-order curves | Equal-Area | US Coast and Geodetic Survey |
| Robinson | Arthur Robinson, 1963
(published 1974) | 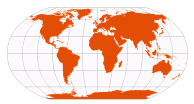 | | Lengths of parallels, central meridian, and pole lines are arbitrarily tabulated for best visual appearance
Parallels are equally spaced between the standard parallels of 38° N/S; spacing decreases towards the poles; no point is distortion-free | | Rand McNally
National Geographic (1988-1998)
CIA (central meridian 10°E) |
| Cube | | 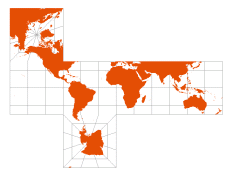 | [Plate Carrée between 45° N/S, abutted Collignon projections for the poles] | There are certainly more elegant cube projections than the one provided by ArcMap; one common approach is to place the poles at opposite corners and use Gnomonic projections for each face | | Homemade holiday decorations |
| Fuller | Buckminster Fuller, 1946 (cuboctohedron), 1954 (icosohedron) | 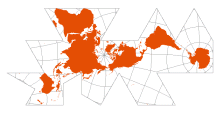 | Dymaxion Map
AirOcean World Map
[Unfolded icosahedron, with each face in gnomonic projection] | No land is cut
No natural “up” direction
The edges of each face are standard lines; no point is distortion-free, but overall distortion is low | | Jasper Johns (1967) |
| ...click here to collapse this table |
| Name | Author, Date | Example, with relevant parameters | Also known as /
[Equivalent to] | Properties | Equal-Area? | Used by /
[Applications] |
| Azimuthal Equidistant | said to be used in ancient Egyptian star maps
fully developed in 15th and 16th centuries | 
centered on: north pole, paris, new york | Postel (1581) | Constant radial scale from central point (i.e., all straight lines through the central point are standard lines)
Distortion-free only at central point | | the Cassinis' floor map at the Paris Observatory (1680s)
United Nations Emblem
Flat Earth Society
[easily computing distances or missile ranges] |
| Equidistant Conic | based on Ptolemy’s 1st Projection, c.100 CE
final form by Joseph Nicholas De l'Isle, 1745 | 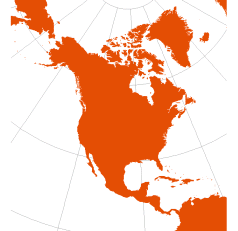
optimize for: world, north america, africa | Simple Conic | Parallels are equally spaced: all meridians are standard, with the same scale as the standard parallels; no distortion along the standard parallels
Special Case: Equidistant Cylindrical results when standard parallels are at or equidistant from the equator | | |
Orthographic
(also listed as “The World From Space” in ArcMap) | used by Hipparchus, 2ndC BCE
renamed “orthographique” by François d'Aiguillon, 1613 | 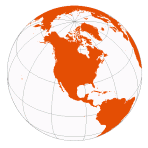
centered on 100°W, 45°N | Azimuthal Orthographic | 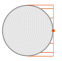
Distortion-free only at central point | | [pictorial views] |
Vertical Perspective
(listed as a “World” projection in ArcMap) | used by Matthias Seutter, 1740 (observer at ~12,750km)
various “far-side” projection points used in 18th and 19th centuries | 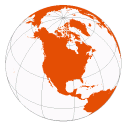
centered on 100°W, 45°N
height of observer: 35,786km
(approximately a geosynchronous orbit) | “Near-Side” Vertical Perspective (Stereographic and Gnomonic being “far-side” projections) | 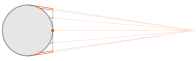
Distortion-free only at central point | | Google Earth
US Weather Service (for satellite data)
[pictorial views] |
| Lambert Conformal Conic | Johann Lambert, 1772 | 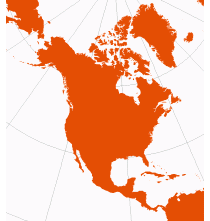
optimize for: world, north america, africa | | Conformal: local angles are preserved, and local circles are not deformed — at every point east/west scale is the same as north/south scale
Distortion is constant along any parallel
Map is infinite in extent
Special Cases: Mercator results when standard parallels are at or equidistant from the equator. Polar Stereographic results when both standard parallels are at one pole. | | The American Oxford Atlas
Rand McNally
National atlases of Canada and Japan
USGS (since 1957) |
| Lambert Azimuthal Equal-Area | Johann Lambert, 1772 | 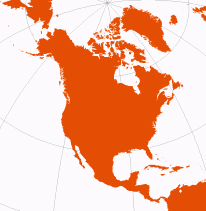
optimize for: north pole, north america, eastern hemisphere | [polar version: Albers Equal-Area Conic with both standard parallels at a pole] | Distortion-free only at central point | Equal-Area | nationalatlas.gov (with central point at 45°N, 100°W) |
Lambert Equal-Area Conic
(in ArcMap, use Albers) | Johann Lambert, 1772 | 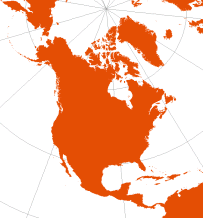
standard parallel at ~48° 35' N
(for Lambert’s own cone constant of ⅞)
optimize for: world, north america, europe | [Albers Equal-Area Conic with one standard parallel at a pole] | No distortion along standard parallel | Equal-Area | superceded by Albers |
| Albers Equal-Area Conic | Heinrich Albers, 1805 | 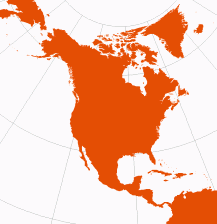
optimize for: world, north america, africa | | No distortion along standard parallels
Special Cases: Lambert Equal-Area Conic results when one standard parallel is at a pole. Polar Azimuthal Equal-Area results when both standard parallels are at one pole. Cylindrical Equal-Area results when both standard parallels are at or equidistant from the equator.
| Equal-Area | USGS (standard parallels at 45.5°N, 29.5°N; central meridian at 96°W)
US Census FactFinder |
| ...click here to collapse this table |
| Name | Author, Date | Example, with relevant parameters | Also known as /
[Equivalent to] | Properties | Equal-Area? | Used by /
[Applications] |
| Azimuthal Equidistant | said to be used in ancient Egyptian star maps
fully developed in 15th and 16th centuries | 
centered on: north pole, paris, new york | Postel (1581) | Constant radial scale from central point (i.e., all straight lines through the central point are standard lines)
Distortion-free only at central point | | the Cassinis' floor map at the Paris Observatory (1680s)
United Nations Emblem
Flat Earth Society
[easily computing distances or missile ranges] |
| Stereographic | used by Hipparchus, 2ndC BCE
renamed “stereographique” by François d'Aiguillon, 1613 | 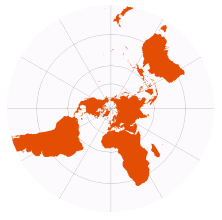
centered on north pole | Azimuthal Stereographic
[Lambert Conformal Conic with both standard parallels at one pole] | 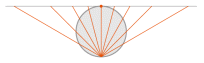
Conformal: local angles are preserved, and local circles are not deformed — at every point east/west scale is the same as north/south scale
All circles are preserved
Loxodromes (constant bearing / rhumb lines) are logarithmic sprials
Distortion-free only at central point
Map is infinite in extent | | [conformal poles or hemispheres]
[oblique versions used to map paths of solar eclipses] |
| Gnomonic | used by Thales, 6thC BCE
renamed “gnomic” by William Emerson, 1749
renamed “gnomonic” by Augustus DeMorgan, 1836 | 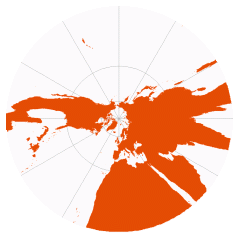
centered on north pole | Central | 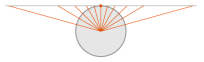
All straight lines are great circles
Distortion-free only at central point
Can only show one hemisphere
Map is infinite in extent | | [plotting shortest route between two points] |
| Mercator | Gerardus Mercator, 1569 |  | Cylindrical Conformal
[Lambert Conformal Conic with standard parallels at or equidistant from the equator] | Conformal: local angles are preserved, and local circles are not deformed — at every point east/west scale is the same as north/south scale
Distortion is constant along any parallel, and any parallel can be defined as standard
Constant bearings (rhumb lines / loxodromes) are straight lines
Map extends infinitely North and South | | Google Maps (note the dynamic scale bar)
[navigating a constant bearing] |
Two-Point Equidistant
(available as a custom projection in ArcMap) | Hans Maurer, 1919
Charles Close, 1921 | 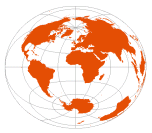
points at: equator, at 60° E/W, new york / sydney | | Distance from any point on the map to either of the two regulating points is accurate (although except for the line connecting the two regulating points, straight lines do not trace great circle paths)
Distortion-free only at the regulating points
When both points are the same, this projection becomes an Azimuthal Equidistant | | National Geographic (for Asia)
Ellipsoidal version by Jay Donald used by AT&T for establishing long-distance rates |
| Loximuthal | Karl Siemon, 1935
Waldo Tobler, 1966 | 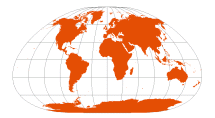
centered on: london, mexico city, sydney | | From the central point (only!), lines of constant bearing (rhumb lines / loxodromes) are straight, and their length is accurate
Parallel through central point is standard, with same scale as central meridian; parallels are equally spaced; distortion-free only where standard parallel intersects the central meridian | | [determining length of rhumb lines — these (usually) do not trace the shortest distance between two points] |
| ...click here to collapse this table |
| Name | Author, Date | Example, with relevant parameters | Also known as /
[Equivalent to] | Properties | Equal-Area? | Used by /
[Applications] |
Equidistant Cylindrical | attributed to Marinus of Tyre, c.100 CE | 
show: world, montana | Equirectangular
[Equidistant Conic with standard parallels equidistant from the equator] | All merdians are standard, with same scale as the standard parallels
No distortion along standard parallels | | Mapquest (standard parallels 37.5° N/S)
Yahoo Maps (standard parallels 51° N/S) |
Cassini
(available as custom projection in ArcMap) | César Cassini, 1745 (for France)
Johann von Soldner, c.1810 (for Germany, Great Britain) | 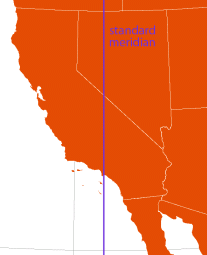
show: world, california
(using spherical coodinates; ArcMap can only plot ellipsoid ±45° from standard meridian) | Cassini-Soldner
[transverse Plate Carrée] | Constant scale perpendicularly away from the standard meridian
No distortion along standard meridian | | British Isles (before c.1920)
[regions with predominating North—South extent] |
| Mercator | Gerardus Mercator, 1569 | 
show: world, montana | Cylindrical Conformal
[Lambert Conformal Conic with standard parallels at or equidistant from the equator] | Conformal: local angles are preserved, and local circles are not deformed — at every point east/west scale is the same as north/south scale
Distortion is constant along any parallel, and any parallel can be defined as standard
Constant bearings (rhumb lines / loxodromes) are straight lines
Map extends infinitely North and South | | Google Maps (note the dynamic scale bar)
[navigating a constant bearing] |
Transverse Mercator
(available in three varieties in ArcMap, all custom projections) | spherical: Johann Lambert, 1772
ellipsoidal: Carl Friedrich Gauss (1822), Louis Krüger (1912) | 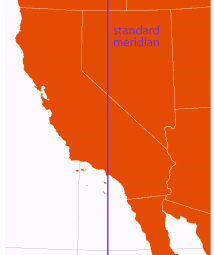
show: world, california
(using spherical coodinates; ArcMap can only plot ellipsoid ±80° from standard meridian) | Gauss-Krüger (ellipsoidal) | Both the sphere- and ellipsoid-based versions are conformal, but with the ellipsoid-based version scale distortion does not increase uniformly away from the standard meridian
No distortion along the standard meridian, and at every point east/west scale is the same as north/south scale
Map extends infinitely East and West | | USGS (with reduced scale factor)
[regions with predominating North—South extent]
Various US State Plane systems — see reference map |
Oblique Mercator
(available as a custom projection in ArcMap) | spherical: Charles Sanders Peirce (1894), Ernst Debes (1895)
most common ellipsoidal equations: Martin Hotine, 1946 | 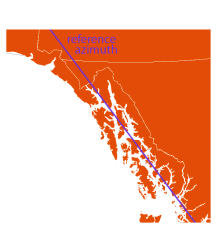
show: world, alaska panhandle | Rectified Skew Orthomorphic
Hotine Oblique Mercator | Hotine’s formulas are conformal, but with an ellipsoid it is impossible to preserve scale along the reference azimuth, and scale does not increase uniformly away from it
Scale is (almost) constant along reference azimuth, and at every point east/west scale is the same as north/south scale
Map extends infinitely away from reference azimuth | | [regions with predominating extent other than North—South or East—West, such as Hawai'i and the Alaska Panhandle] |
| Lambert Conformal Conic | Johann Lambert, 1772 | 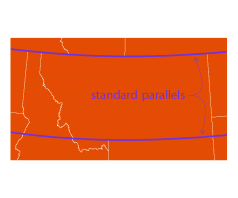
show: world, montana | | Conformal: local angles are preserved, and local circles are not deformed — at every point east/west scale is the same as north/south scale
Distortion is constant along any parallel
Map is infinite in extent
Special Cases: Mercator results when standard parallels are at or equidistant from the equator. Polar Stereographic results when both standard parallels are at one pole. | | The American Oxford Atlas
Rand McNally
National atlases of Canada and Japan
USGS (since 1957)
Various US State Plane systems — see reference map |
Polyconic
(listed as a “World” projection in ArcMap) | Ferdinand Hassler, c.1820 | 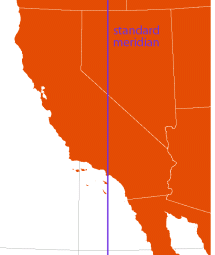
optimize for: world, north america, california | American Polyconic (to distinguish it from various “modified polyconic” projections)
[Bonne with every parallel drawn as a reference parallel] | All parallels are standard and circular, with the same scale as the central meridian
No distortion along the central meridian
(This projection is essentially obsolete, its major benefit having been ease of construction with numerical tables.) | | US Coast and Geodetic Survey, using ellipsoidal form (until c.1920)
USGS (until 1957) |
| ...click here to collapse this table |